El par de funciones lógicas que veremos hoy nos permiten evaluar distintas condiciones de forma simultánea. Ambas generan un resultado booleano (VERDADERO o FALSO) que usualmente servirá como argumento de otras funciones lógicas.
Sintaxis función Y
=Y(valor lógico1, [valor lógico2,...])
Los argumentos serán expresiones creadas con valores, matrices, referencias u otros valores lógicos hasta un máximo de 255 condiciones. Al menos un argumento debe pasarse a la función. Esta es la razón de que sólo el primer argumento sea obligatorio y los argumentos del 2 al 255 sean opcionales. Los valores o celdas vacías serán ignorados.
Usualmente, esta función la veremos utilizada en conjunto con la función SI u otras funciones que requieran valores booleanos (VERDADERO o FALSO), ya que su resultado será, de la misma forma, uno de ambos valores.
Múltiples condiciones
En el caso de la función Y, cada uno de los argumentos es una condición por evaluar y el resultado será VERDADERO si la evaluación de cada argumento o condición es verdadera. De manera ilustrativa veamos los siguientes resultados:

Como podemos observar, sólo la última fórmula genera un resultado VERDADERO, ya que todos y cada uno de los argumentos son a su vez verdaderos.
Ahora, de forma práctica, digamos que tenemos los datos para evaluar algunas acciones y decidir en cuales invertir. Deseamos revisar las acciones que han pagado sus últimos dividendos mayores a $0.6, cuya diferencia entre último precio y el promedio anual sea mayor a 3 y, finalmente, que posean una tendencia de compra.
De acuerdo con este planteamiento, es evidente que queremos evaluar tres condiciones distintas para decidir si revisaremos en detalle la acción como prospecto a invertir o la descartaremos. Crearemos la fórmula como vemos a continuación:
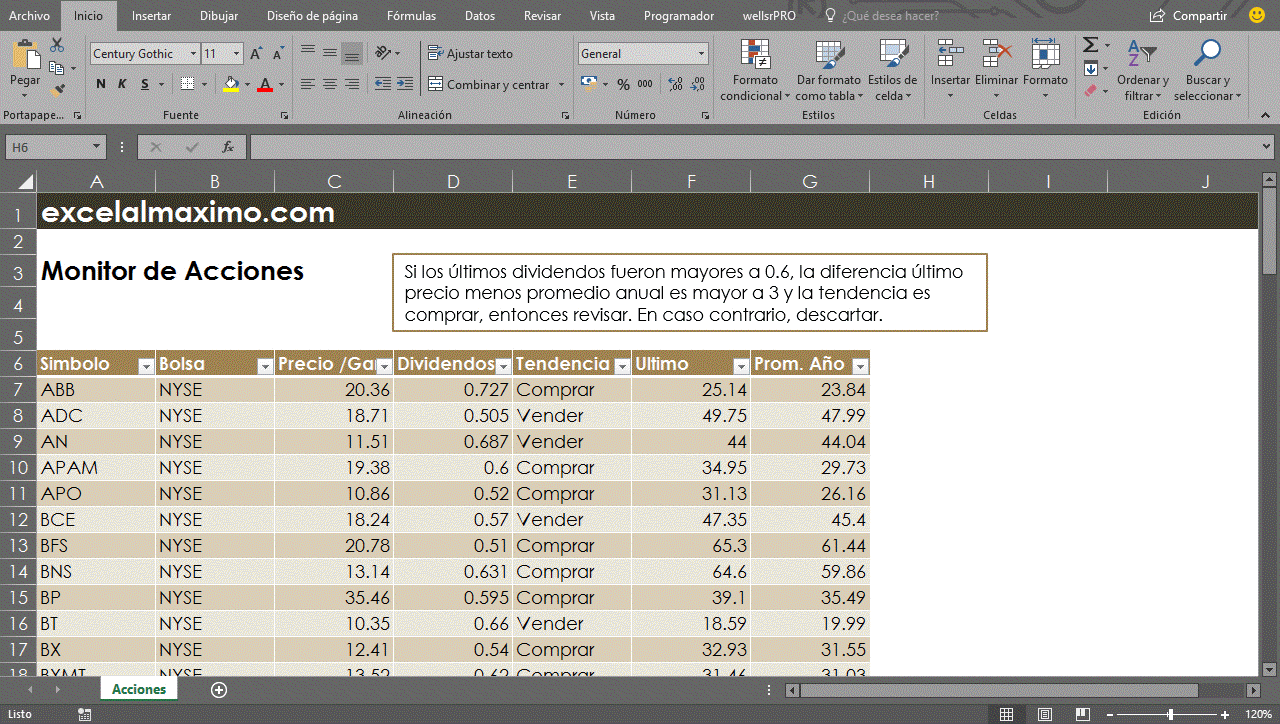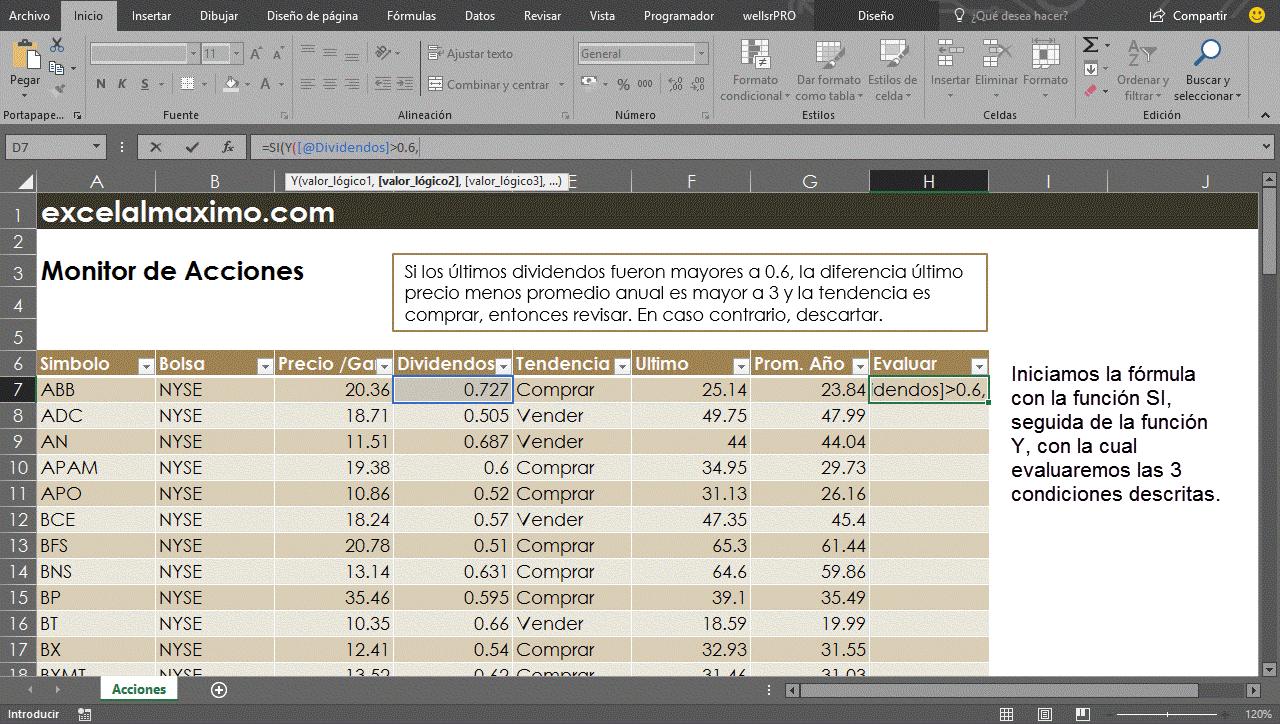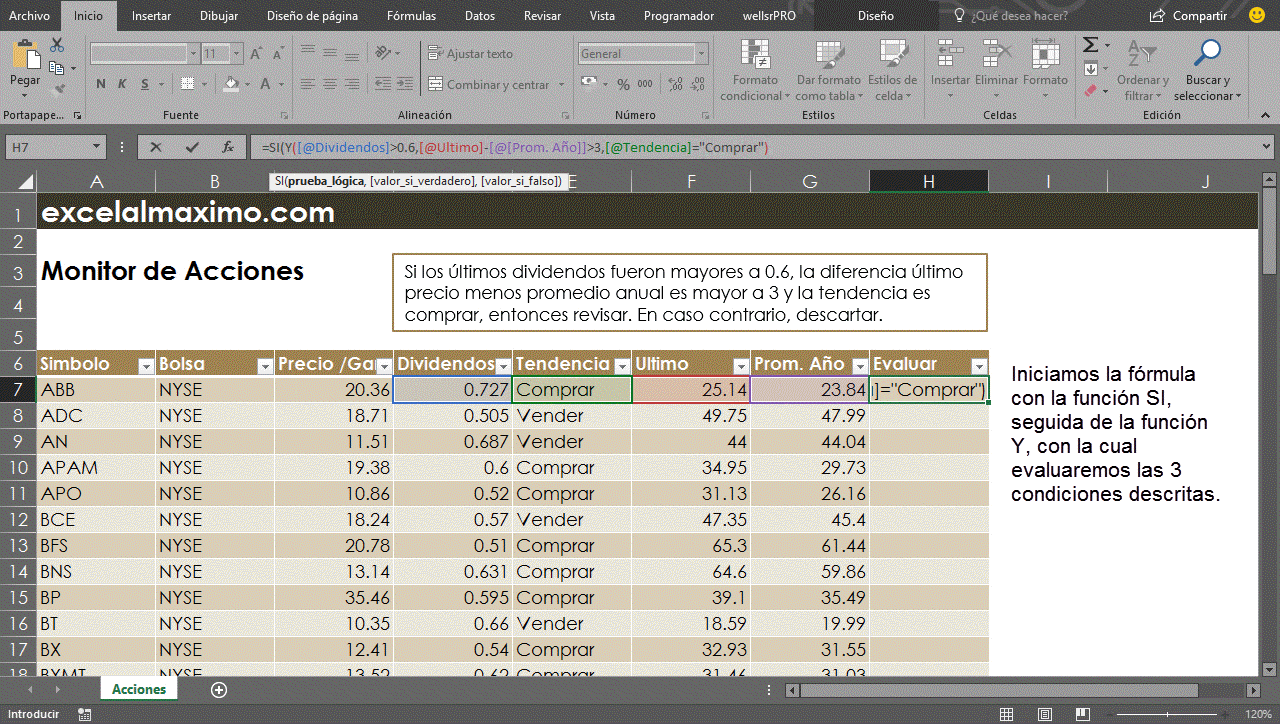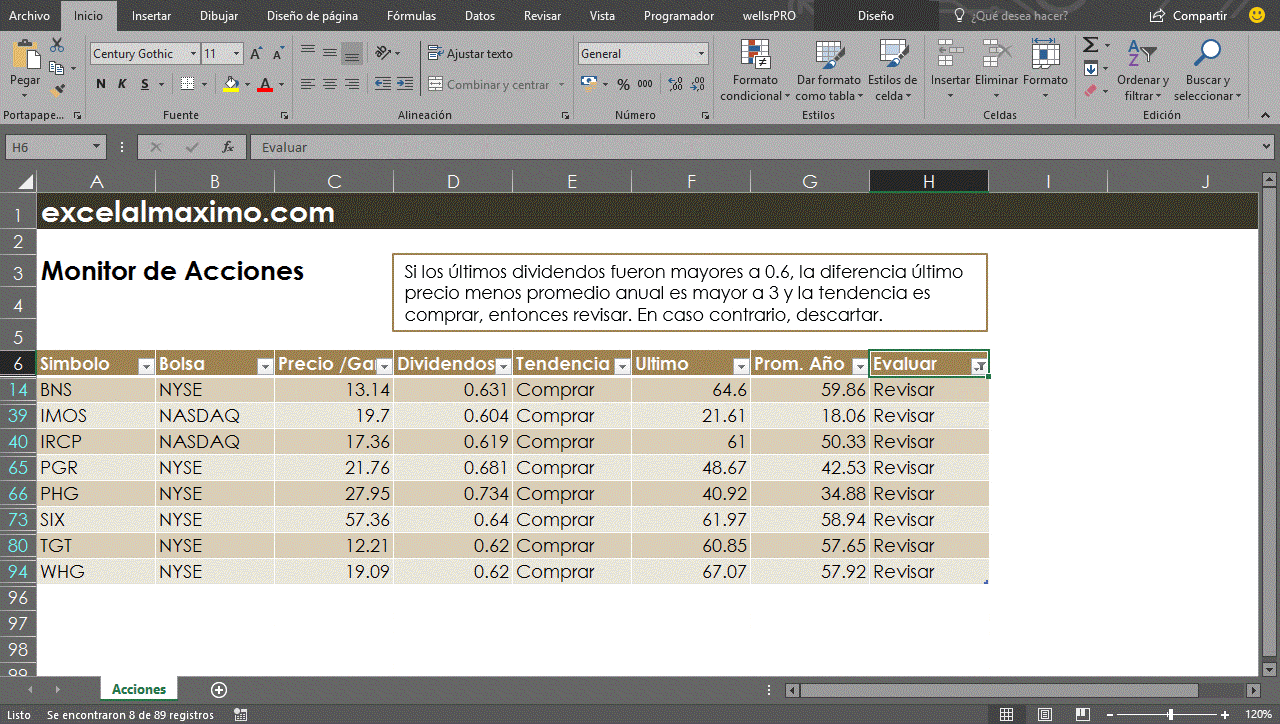
Fácilmente podemos observar que con una simple construcción SI / Y, podemos evaluar tres condiciones y así llegar a los datos que nos interesan.
Para continuar, de la misma forma que tenemos una función lógica para las operaciones Y, también tenemos una función para la operación O.
Sintaxis función O
=O(valor lógico1, [valor lógico2,...])
Al igual que la función Y, esta evalúa de 1 a 255 argumentos que serán valores, matrices, referencias u otros valores lógicos. Los valores y celdas vacíos son ignorados.
La diferencia con la función anterior es que la función O resulta en un valor booleano VERDADERO, si al menos una de las condiciones en sus argumentos es verdadera.

Observemos que, en el segundo caso, un solo argumento verdadero genera que toda la expresión resulte en el valor booleano VERDADERO.
Funciones Y/O anidadas
Modificando nuestro ejemplo para demostrar la función O, podemos hacer lo siguiente. Recordemos las condiciones originales:
Si los últimos dividendos fueron mayores a 0.6 y la diferencia último precio menos promedio anual es mayor a 3 y la tendencia es comprar, entonces revisar. En caso contrario, descartar.
Si cambiamos las dos primeras condiciones y decimos que sólo una de ellas basta que sea verdadera para revisar la acción, tendríamos lo siguiente:
Si los últimos dividendos fueron mayores a 0.6 o la diferencia último precio menos promedio anual es mayor a 3 y la tendencia es comprar, entonces revisar. En caso contrario, descartar.
Aunque hemos cambiado una sola palabra (…dividendos fueron mayores a 0.6 o la diferencia último…), nuestras condiciones ahora deben expresarse con una fórmula distinta. Veamos cómo construirla:
La fórmula, con referencias estructuradas de una tabla, queda como sigue:
=SI(Y(O([@Dividendos]>6,[@Ultimo]-[@[Prom. Año]]>3),[@Tendencia]="Comprar"),"Revisar","Descartar")
Si observamos con detalle, en nuestros criterios mantuvimos la tercera condición. Por esta razón todavía se requiere del uso de la función Y al inicio y de la función O de forma anidada.
Como siempre, recomiendo hacer un pequeño esquema de la lógica que debe tener nuestra fórmula antes de implementarla, ya que esto evitará errores y nos permitirá comprender a cabalidad los detalles de cada fórmula y función que utilicemos.
Hasta aquí llega esta parte de la serie de las 41 funciones de Excel que debes dominar. Espero ya estén implementando y practicando estas funciones en su día a día con Excel, hasta la próxima entrada.
